Optical Flow Tracker

Crafted by Bob Bu · Spring 2025

This is an OpenCV project that tracks feature points in video using optical flow for motion visualization and computer vision tracking. The gradient-based pipeline first compute temporal and spatial derivatives, then solve for the flow vector u=[u,v]T\mathbf{u}=[u,v]^T over a window or over patches.

Frame 1 (car_1)Frame 2 (car_2)

For two consecutive grayscale frames I1I_1 and I2I_2, the temporal gradient is computed as the frame difference

It(x,y)=I2(x,y)−I1(x,y). I_t(x,y)=I_2(x,y)-I_1(x,y).

A threshold on It(x,y)I_t(x,y) helps isolate motion-dominant changes and suppress low-amplitude noise before solving for motion.

Thresholded temporal gradient

Spatial gradients are computed using forward differences along the horizontal and vertical axes

Ix(x,y)=I(x+1,y)−I(x,y),Iy(x,y)=I(x,y+1)−I(x,y). \begin{aligned} I_x(x,y) &= I(x+1,y)-I(x,y),\\ I_y(x,y) &= I(x,y+1)-I(x,y). \end{aligned}
Spatial gradient IxSpatial gradient Iy

With IxI_x, IyI_y, and ItI_t, the optical flow constraint is written as

Ixu+Iyv=−It. I_x u + I_y v = -I_t.

Solving this relation within a selected region yields a motion vector field.

Quiver plot of the flow field

Single-window flow assumes motion is approximately uniform inside the window, which can fail when multiple objects move differently or when motion contains rotation or scale changes.

To improve stability, the image can be divided into non-overlapping patches of size block_size×block_size\text{block\_size}\times\text{block\_size}. A single flow vector is solved per patch, representing average motion within that region. Increasing block_size\text{block\_size} reduces noise by averaging over a larger area, while decreasing it preserves finer motion detail.

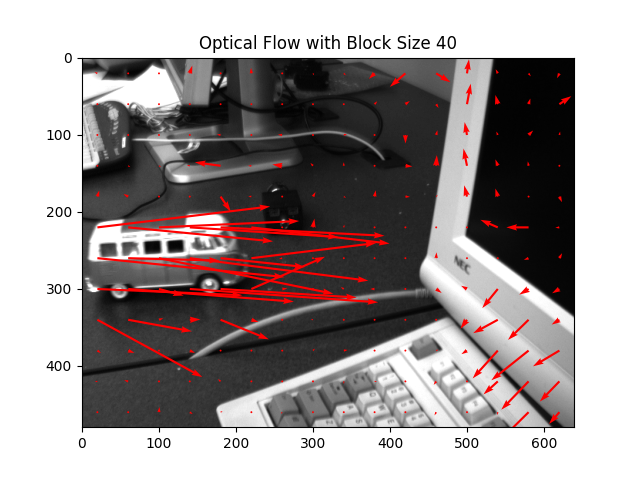
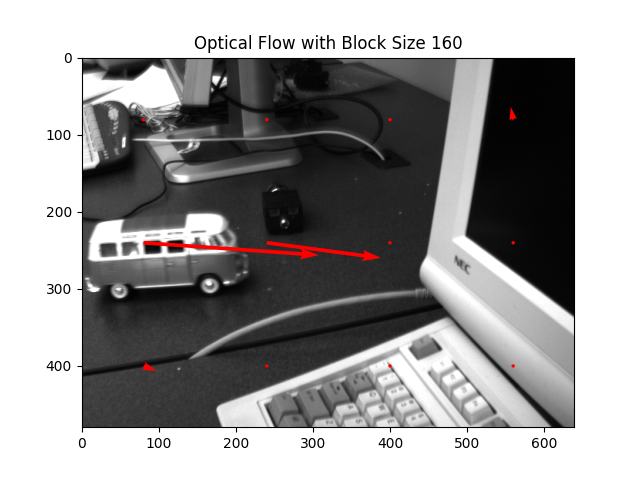
Quiver plot of the flow fieldQuiver plot of the flow fieldQuiver plot of the flow fieldQuiver plot of the flow field

For a given video, the tracker runs frame-by-frame and renders motion vectors on top of the video. Optical flow works best when brightness is approximately constant, motion between frames is small, and nearby pixels share similar motion.

A good example is when the motion is smooth and small between consecutive frames. Brightness constancy holds as the video has consistent lighting. The scene contains smooth spatial changes.

A bad example violates the small motion assumption: Rapid movements lead to inaccurate vectors. Brightness constancy is violated due to changing lighting or shadows. Complex scenes with multiple overlapping motions violate the spatial smoothness assumption.

Beyond translation, this project also explores rotation and zoom using gradients tailored to angular and scale change, then solves an optical-flow-like constraint for rotation rr and scale ss.

Irr+Iss=−It. I_r r + I_s s = -I_t.
Motion vectors for rotation and scale

The derivation relies on a first-order Taylor expansion, assuming higher-order terms are negligible under small motion. A common linearization is

I(x+u,y+v,t+1)≈I(x,y,t)+Ixu+Iyv+It. \begin{aligned} I(x+u,y+v,t+1) &\approx I(x,y,t) \\ &\quad + I_x u + I_y v + I_t. \end{aligned}

When motion is large or intensity changes abruptly, higher-order terms become non-negligible and the linear approximation degrades.

University of Alberta · Edmonton, AB, Canada